Sword-For-Offer

发表于 | 分类于

引言：

LeetCode Top100 tags题解

P39数组中重复数字

要求时间复杂度 O(N)，空间复杂度 O(1)。因此不能使用排序的方法，也不能使用额外的标记数组。对于这种数组元素在 [0, n-1] 范围内的问题，可以将值为 i 的元素调整到第 i 个位置上进行求解。以 (2, 3, 1, 0, 2, 5) 为例，遍历到位置 4 时，该位置上的数为 2，但是第 2 个位置上已经有一个 2 的值了，因此可以知道 2 重复：

思路

　　从哈希表的思路拓展，重排数组：把扫描的每个数字（如数字m）放到其对应下标（m下标）的位置上，若同一位置有重复，则说明该数字重复。

img

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
package swordforoffer;

/**
 * @description: 数组中重复数字
 * @author: zw
 * @createDate: 2020/2/11
 * @version: 1.0.0
 */
public class Solution03 {

    public int findDuplicate(int[] arr){
        // 输入判断
        if (arr == null || arr.length <= 0) {
            System.out.println("数组输入无效！");
            return -1;
        }
        for (int a : arr) {
            if (a < 0 || a > arr.length - 1) {
                System.out.println("数字大小超出范围！");
                return -1;
            }
        }

        // 查找函数
        for (int i = 0; i < arr.length; i++) {
            while(arr[i] != i){
                if(arr[arr[i]] == arr[i]){
                    return arr[i];
                }
                /*
                 * int temp = arr[i];
                 * arr[i] = arr[arri]];
                 * arr[arr[i]] = temp;
                 * 这种写法会造成死循环
                 */
                int temp = arr[i];
                arr[i] = arr[temp];
                arr[temp] = temp;
            }
        }
        System.out.println("数组中无重复数字！");
        return -1;
    }

    // ==================================测试代码==================================
    /*
     *数组为null
     */
    public void test1() {
        System.out.print("test1：");
        int[] a = null;
        int dup = findDuplicate(a);
        if (dup >= 0)
            System.out.println("重复数字为：" + dup);
    }

    /*
     *数组无重复数字
     */
    public void test2() {
        System.out.print("test2：");
        int[] a = { 0, 1, 2, 3 };
        int dup = findDuplicate(a);
        if (dup >= 0)
            System.out.println("重复数字为：" + dup);
    }

    /*
     *数组数字越界
     */
    public void test3() {
        System.out.print("test3：");
        int[] a = { 1, 2, 3, 4 };
        int dup = findDuplicate(a);
        if (dup >= 0)
            System.out.println("重复数字为：" + dup);
    }

    /*
     *数组带重复数字
     */
    public void test4() {
        System.out.print("test4：");
        int[] a = { 1, 2, 3, 2, 4 };
        int dup = findDuplicate(a);
        if (dup >= 0)
            System.out.println("重复数字为：" + dup);
    }

    public static void main(String[] args) {
        Solution03 f = new Solution03();
        f.test1();
        f.test2();
        f.test3();
        f.test4();
    }
}

P44二维数组查找

解题思路

要求时间复杂度 O(M + N)，空间复杂度 O(1)。其中 M 为行数，N 为 列数。该二维数组中的一个数，小于它的数一定在其左边，大于它的数一定在其下边。因此，从右上角开始查找，就可以根据 target 和当前元素的大小关系来缩小查找区间，当前元素的查找区间为左下角的所有元素。

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
package swordforoffer;

/**
 * @description: 二维数组中查找数据
 * 基本思想是沿对角线横切或者竖切判断。
 * @author: zw
 * @createDate: 2020/1/27
 * @version: 1.0.0
 */
public class Solution01 {
    public boolean find(int target, int[][] array) {

        int row = array.length;         // 行
        int column = array[0].length;   // 列

        // 从右上角开始定义索引
        int r = 0;
        int c = column - 1;
        // "while(true){...}"记住条件是true的
        while (r < row && c > -1) {
            if (array[r][c] == target)
                return true;
            if (array[r][c] > target)
                c--;
            else
                r++;
        }
        return false;
    }
}

P51替换空格

题目

　　请实现一个函数，把字符串中的每个空格替换成”%20”。例如输入“We are happy.”，则输出“We%20are%20happy.”。

思路

　　首先要询问面试官是新建一个字符串还是在原有的字符串上修改，本题要求在原有字符串上进行修改。

　　若从前往后依次替换，在每次遇到空格字符时，都需要移动后面O(n)个字符，对于含有O(n)个空格字符的字符串而言，总的时间效率为O(n2)。

　　转变思路：先计算出需要的总长度，然后从后往前进行复制和替换，则每个字符只需要复制一次即可。时间效率为O(n)。

测试用例

  1. 字符串中无空格
  2. 字符串中含有空格（连续空格，空格在首尾等）
  3. 字符串为空字符串或者为null
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
package swordforoffer;

/**
 * @description: 替换空格
 * @author: zw
 * @createDate: 2020/1/28
 * @version: 1.0.0
 */
public class Solution05 {

    // 使用Java内置函数
    public String replaceSpace1(StringBuffer str) {
        if (str == null) {
            System.out.println("输入错误！");
            return null;
        }
        return str.toString().replace(" ", "%20");
    }

    // 新建一个字符串
    public String replaceSpace2(StringBuffer str) {
        if (str == null) {
            System.out.println("输入错误！");
            return null;
        }

        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < str.length(); i++) {
            char c = str.charAt(i);
            if (c == ' ')
                sb.append("%20");
            else
                sb.append(c);
        }
        return sb.toString();
    }
    // 补充：StringBuilder/StringBuffer是可变的，其中StringBuffer是线程安全的，
    // StringBuilder是线程不安全的，所以效率更高。其中字符串的拼接操作的原理是生
    // 成一个新的StringBuffer来append的。

    // 在原字符串上修改
    public String replaceSpace3(StringBuffer str) {
        if (str == null) {
            System.out.println("输入错误！");
            return null;
        }

        // 原始字符串长度
        int len1 = str.length();
        for (int i = 0; i < len1; i++) {
            if (str.charAt(i) == ' ') {
                //len += 2;
                str.append("  ");
            }
        }
        // 更改后字符串长度
        int len2 = str.length();
        // 从后向前填入
        int indexOld = len1 - 1;
        int indexNew = len2 - 1;
        while (indexNew > indexOld) {
            char c = str.charAt(indexOld);
            if (c == ' ') {
                str.setCharAt(indexNew--, '0');
                str.setCharAt(indexNew--, '2');
                str.setCharAt(indexNew--, '%');
            } else
                str.setCharAt(indexNew--, c);
            indexOld--;
        }
        return str.toString();
    }

    // ==================================测试代码==================================

    /*
     * 输入为null
     */
    public void test1() {
        System.out.print("Test1：");
        StringBuffer sBuffer = null;
        String s = replaceSpace3(sBuffer);
        System.out.println(s);
    }

    /*
     * 输入为空字符串
     */
    public void test2() {
        System.out.print("Test2：");
        StringBuffer sBuffer = new StringBuffer("");
        String s = replaceSpace3(sBuffer);
        System.out.println(s);
    }

    /*
     * 输入字符串无空格
     */
    public void test3() {
        System.out.print("Test3：");
        StringBuffer sBuffer = new StringBuffer("abc");
        String s = replaceSpace3(sBuffer);
        System.out.println(s);
    }

    /*
     * 输入字符串为首尾空格，中间连续空格
     */
    public void test4() {
        System.out.print("Test4：");
        StringBuffer sBuffer = new StringBuffer(" a b  c  ");
        String s = replaceSpace3(sBuffer);
        System.out.println(s);
    }

    public static void main(String[] args) {
        Solution05 rs = new Solution05();
        rs.test1();
        rs.test2();
        rs.test3();
        rs.test4();
    }
}

P59从尾到头输出链表

思路

　　结点遍历顺序只能从头到尾，但是输出的顺序却为从尾到头，是典型的“后进先出”问题，这就要联想到使用栈，从而也可以联想到使用递归。

测试用例

　　1.功能测试（单个结点链表，多个结点链表）

　　2.特殊输入测试（链表为空）

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
package swordforoffer;

import java.util.ArrayList;
import java.util.Collections;
import java.util.Stack;

/**
 * @description: 反转打印链表
 * @author: zw
 * @createDate: 2020/1/28
 * @version: 1.0.0
 */
public class Solution06 {

    // 使用Java内置函数
    public void reverseList1(ArrayList arrayList) {
        Collections.reverse(arrayList);
        System.out.println(arrayList);
    }

    // 自己写的函数，非递归方式
    public ArrayList<Integer> reverseList2(ListNode listNode) {
        ArrayList<Integer> list = new ArrayList<>();
        ListNode temp = listNode;
        while (temp != null) {
            list.add(0, temp.val);
            temp = temp.next;
        }
        return list;
    }


    // 递归方式
    ArrayList<Integer> list3 = new ArrayList();
    public ArrayList<Integer> reverseList3(ListNode listNode) {

        if (listNode != null) {
            reverseList3(listNode.next);
            list3.add(listNode.val);
        }
        return list3;
    }

    // 使用栈方式
    public ArrayList<Integer> reverseList4(ListNode listNode) {
        ArrayList<Integer> list = new ArrayList<>();
        Stack<ListNode> stack = new Stack<>();
        while (listNode != null) {
            stack.push(listNode);
            listNode = listNode.next;
        }

        while (!stack.isEmpty()) {
            list.add(stack.pop().val);
        }
        return list;
    }

    // ==================================测试代码==================================
    /* 
     * 链表为空时
     */
    public void test1() {
        ListNode listNode = null;
        System.out.println("采用非递归方式(list头插入)：");
        System.out.println(reverseList2(listNode));
        System.out.println("采用递归方式：");
        System.out.println(reverseList3(listNode));
        System.out.println("采用栈方式：");
        System.out.println(reverseList4(listNode));

    }

    /*
     * 多节点链表测试
     */
    public void test2() {
        ListNode ListNode1 = new ListNode(1);
        ListNode ListNode2 = new ListNode(2);
        ListNode ListNode3 = new ListNode(3);
        ListNode ListNode4 = new ListNode(4);
        ListNode ListNode5 = new ListNode(5);
        ListNode1.next=ListNode2;
        ListNode2.next=ListNode3;
        ListNode3.next=ListNode4;
        ListNode4.next=ListNode5;
        System.out.println("采用非递归方式(list头插入)：");
        System.out.println(reverseList2(ListNode1));
        System.out.println("采用递归方式：");
        System.out.println(reverseList3(ListNode1));
        System.out.println("采用栈方式：");
        System.out.println(reverseList4(ListNode1));

    }

    /**
     * 单个结点链表
     */
    public void test3() {
        ListNode ListNode1 = new ListNode(1);
        System.out.println("采用非递归方式(list头插入)：");
        System.out.println(reverseList2(ListNode1));
        System.out.println("采用递归方式：");
        System.out.println(reverseList3(ListNode1));
        System.out.println("采用栈方式：");
        System.out.println(reverseList4(ListNode1));

    }

    public static void main(String[] args) {
        Solution06 demo = new Solution06();
        System.out.println("test1:");
        demo.test1();
        System.out.println("test2:");
        demo.test2();
        System.out.println("test3:");
        demo.test3();
    }
}

总结：

  1. 对于“后进先出”问题，要快速想到”栈“，也同时想到递归。
  2. 递归代码的写法，错了好几次。

P62重建二叉树

题目

　　输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1, 2, 4, 7, 3, 5, 6, 8}和中序遍历序列{4, 7, 2, 1, 5, 3, 8, 6}，则重建出其二叉树并输出它的头结点。

思路

　　前序遍历第一个值就是根结点的值，根据该值在中序遍历的位置，可以轻松找出该根结点左右子树的前序遍历和中序遍历，之后又可以用同样方法构建左右子树，所以该题可以采用递归的方法完成。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
package swordforoffer;


import sun.reflect.generics.tree.Tree;

import java.util.Arrays;

/**
 * @description: 重建二叉树，已知前序和中序的情况下
 * @author: zw
 * @createDate: 2020/1/28
 * @version: 1.0.0
 */
public class Solution07 {
    // 递归思想：返回值——树头结点，参数——前序中序数组，
    public TreeNode reConstructBT(int[] pre, int[] front) {

        if (pre == null || front == null) {
            return null;
        }
        if (pre.length == 0 || front.length == 0) {
            return null;
        }
        if (pre.length != front.length) {
            return null;
        }

        // 设置根节点
        TreeNode root = new TreeNode(pre[0]);

        // 遍历中序数组，从中寻找前序数组的第一个节点
        for (int i = 0; i < front.length; i++) {
            if (front[i] == pre[0]) {
                // 递归传给根节点左右子节点
                // 递归左子树参数1：前序数组开始截止到查询到前序数组索引0值，2：中序数组中前序数组第一个值左边
                root.left = reConstructBT(Arrays.copyOfRange(pre, 1, i + 1),
                        Arrays.copyOfRange(front, 0, i));
                // 递归右子树参数：前序中序剩余元素
                root.right = reConstructBT(Arrays.copyOfRange(pre, i + 1, pre.length),
                        Arrays.copyOfRange(front, i + 1, front.length));
                // 查询到根节点递归后就直接返回
                break;
            }
        }
        return root;
    }

    // 树的前序遍历
    public void preOrderTraverse(TreeNode node) {
        // 我写的前序
        //while (node!= null){
        //    System.out.println(node.val);
        //    preOrderTraverse(node.left);
        //    preOrderTraverse(node.right);
        //}
        // 改的前序
        if (node == null)
            return;
        System.out.print(node.val + ", ");
        preOrderTraverse(node.left);
        preOrderTraverse(node.right);
    }

    // 树的中序遍历
    public void inOrderTraverse(TreeNode node) {
        if (node == null)
            return;
        inOrderTraverse(node.left);
        System.out.print(node.val + ", ");
        inOrderTraverse(node.right);
    }


    // ==================================测试代码==================================
    /*
     * 正常二叉树
     */
    public void test1() {
        int[] pre = {1, 2, 4, 7, 3, 5, 6, 8};
        int[] in = {4, 7, 2, 1, 5, 3, 8, 6};
        TreeNode root = reConstructBT(pre, in);
        System.out.println("test1:");
        System.out.println("前序：");
        preOrderTraverse(root);
        System.out.println();
        System.out.println("中序:");
        inOrderTraverse(root);
        System.out.println();
    }

    /*
     * 左斜树
     */
    public void test2() {
        int[] pre = {1, 2, 3, 4, 5};
        int[] in = {5, 4, 3, 2, 1};
        TreeNode root = reConstructBT(pre, in);
        System.out.println("test2:");
        System.out.println("前序：");
        preOrderTraverse(root);
        System.out.println();
        System.out.println("中序:");
        inOrderTraverse(root);
        System.out.println();
    }

    /*
     * 右斜树
     */
    public void test3() {
        int[] pre = {1, 2, 3, 4, 5};
        int[] in = {1, 2, 3, 4, 5};
        TreeNode root = reConstructBT(pre, in);
        System.out.println("test3:");
        System.out.println("前序：");
        preOrderTraverse(root);
        System.out.println();
        System.out.println("中序:");
        inOrderTraverse(root);
        System.out.println();
    }

    /*
     * 单个结点
     */
    public void test4() {
        int[] pre = {1};
        int[] in = {1};
        TreeNode root = reConstructBT(pre, in);
        System.out.println("test4:");
        System.out.println("前序：");
        preOrderTraverse(root);
        System.out.println();
        System.out.println("中序:");
        inOrderTraverse(root);
        System.out.println();
    }

    /*
     * 数组为空
     */
    public void test5() {
        int[] pre = {};
        int[] in = {};
        TreeNode root = reConstructBT(pre, in);
        System.out.println("test5:");
        System.out.println("前序：");
        preOrderTraverse(root);
        System.out.println();
        System.out.println("中序:");
        inOrderTraverse(root);
        System.out.println();
    }

    public static void main(String[] args) {
        Solution07 demo = new Solution07();
        demo.test1();
        demo.test2();
        demo.test3();
        demo.test4();
        demo.test5();
    }
}

P65二叉树的下一个节点

题目

　　给定一棵二叉树和其中的一个结点，如何找出中序遍历顺序的下一个结点？ 树中的结点除了有两个分别指向左右子结点的指针以外，还有一个指向父结点的指针。

解题思路

① 如果一个节点的右子树不为空，那么该节点的下一个节点是右子树的最左节点；

img

② 若当前结点无右子树时，

  • 若当前结点为其父结点的左子结点时，其下一个结点为其父结点；
  • 若当前结点为其父结点的右子结点时，继续向上遍历父结点的父结点，直到找到一个结点是其父结点的左子结点（与① 中判断相同），该结点即为下一结点。

img

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
package swordforoffer;

/**
 * @description: 二叉树下一节点
 * @author: zw
 * @createDate: 2020/2/12
 * @version: 1.0.0
 */
public class Solution08 {

    public TreeLinkNode getNext(TreeLinkNode node) {

        if (node == null) {
            System.out.print("结点为null ");
            return null;
        }

        // 节点有右子树时，下一个节点是向下找
        if (node.right != null) {
            node = node.right;
            while (node.left != null) {
                node = node.left;
            }
            return node;
        }

        // 节点无右子树时，向上找
        while (node.parent != null) {
            // 如果节点无右子树，且是父节点的左子树时，返回其父节点
            if (node.parent.left == node) {
                return node.parent;
            }
            // 向上寻找一个节点，这个节点满足上面的if
            node = node.parent;
        }
        return null;
    }

    // ==================================测试代码==================================
    //创建树较为繁琐，未包括所有测试代码。
    public void test1() {
        TreeLinkNode node = null;
        TreeLinkNode nextNode = getNext(node);
        if (nextNode != null)
            System.out.println(nextNode.val);
        else
            System.out.println("无下一结点");
    }

    public void test2() {
        TreeLinkNode node1 = new TreeLinkNode(1);
        TreeLinkNode node2 = new TreeLinkNode(2);
        TreeLinkNode node3 = new TreeLinkNode(3);
        TreeLinkNode node4 = new TreeLinkNode(4);
        node1.left = node2;
        node1.right = node3;
        node2.parent = node1;
        node3.parent = node1;
        node4.left = node1;
        node1.parent = node4;
        TreeLinkNode nextNodeOf1 = getNext(node1);
        TreeLinkNode nextNodeOf2 = getNext(node2);
        TreeLinkNode nextNodeOf3 = getNext(node3);
        TreeLinkNode nextNodeOf4 = getNext(node4);
        if (nextNodeOf1 != null)
            System.out.println("1结点的下一个结点值为：" + nextNodeOf1.val);
        else
            System.out.println("1结点无下一结点");
        if (nextNodeOf2 != null)
            System.out.println("2结点的下一个结点值为：" + nextNodeOf2.val);
        else
            System.out.println("2结点无下一结点");
        if (nextNodeOf3 != null)
            System.out.println("3结点的下一个结点值为：" + nextNodeOf3.val);
        else
            System.out.println("3结点无下一结点");
        if (nextNodeOf4 != null)
            System.out.println("4结点的下一个结点值为：" + nextNodeOf4.val);
        else
            System.out.println("4结点无下一结点");
    }

    public static void main(String[] args) {
        Solution08 demo = new Solution08();
        System.out.print("test1:");
        demo.test1();
        System.out.print("test2:");
        demo.test2();
    }
}

P68使用两个栈实现队列

思路

in 栈用来处理入栈（push）操作，out 栈用来处理出栈（pop）操作。一个元素进入 in 栈之后，出栈的顺序被反转。当元素要出栈时，需要先进入 out 栈，此时元素出栈顺序再一次被反转，因此出栈顺序就和最开始入栈顺序是相同的，先进入的元素先退出，这就是队列的顺序。

img

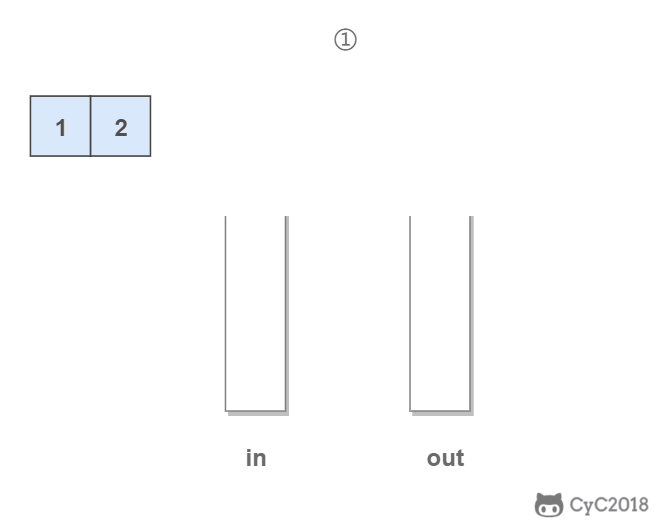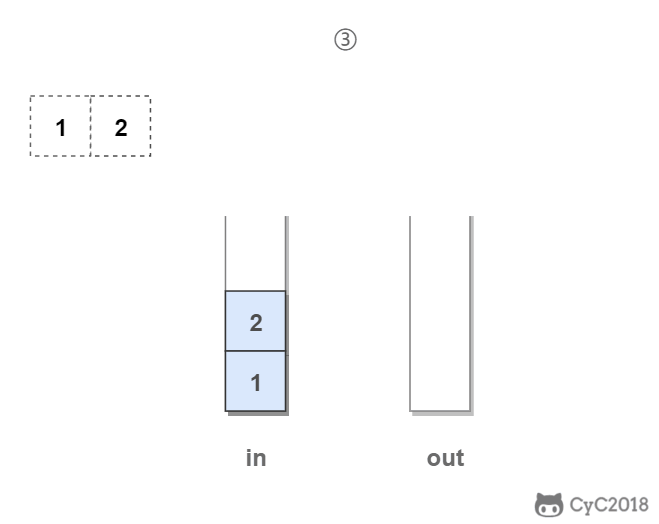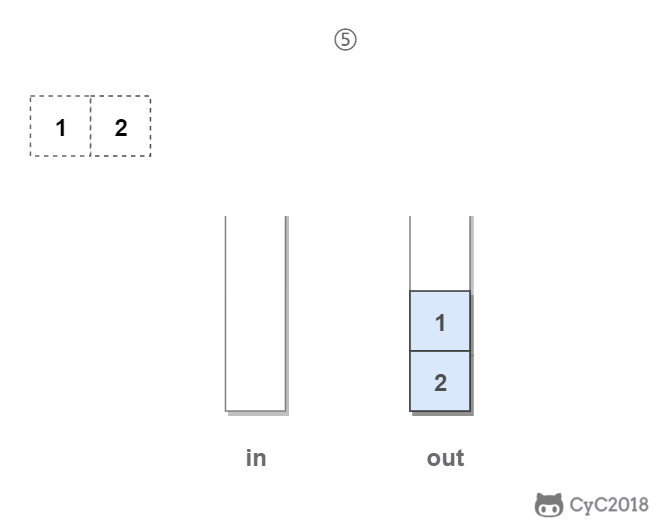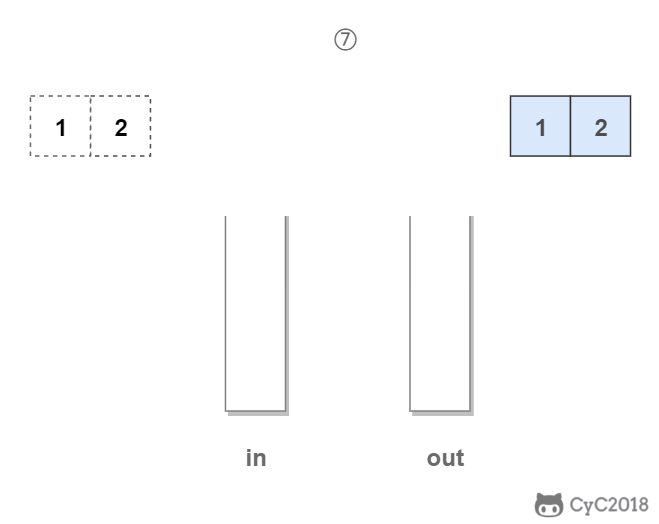
代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
package swordforoffer;

import java.util.Stack;

/**
 * @description: 两个栈实现队列
 * @author: zw
 * @createDate: 2020/1/29
 * @version: 1.0.0
 */
public class Solution09 {


    class Queue {

        // 先定义两个栈
        Stack<Integer> stack1 = new Stack<>();
        Stack<Integer> stack2 = new Stack<>();

        // 实现pop和push的功能
        // 入队使用stack1
        public void push(int node) {
            stack1.push(node);
        }

        // 出队使用stack2
        public int pop() {
            if (stack2.isEmpty()) {
                // 出队是stack2，先查看是否为空
                // 为空情况下再从stack1中调出存入
                // 从stack1中调值时一次性取完
                if (stack1.isEmpty())
                    throw new RuntimeException("队列为空！");
                else {
                    while (!stack1.isEmpty()) {
                        stack2.push(stack1.pop());
                    }
                }
            }
            return stack2.pop();
        }
    }

    //=======测试代码==========

    public void test1() {
        Queue queue = new Queue();
        queue.push(1);
        queue.push(2);
        System.out.println(queue.pop());
        queue.push(3);
        System.out.println(queue.pop());
        System.out.println(queue.pop());
    }

    /*
     * 往空队列删除元素
     */
    public void test2() {
        Queue queue = new Queue();
        System.out.println(queue.pop());
    }

    public static void main(String[] args) {
        Solution09 demo = new Solution09();
        demo.test1();
        demo.test2();
    }
}

P74斐波那契数列

斐波那契数列

image-20200212142801214

解题思路

如果使用递归求解，会重复计算一些子问题。例如，计算 f(4) 需要计算 f(3) 和 f(2)，计算 f(3) 需要计算 f(2) 和 f(1)，可以看到 f(2) 被重复计算了。

img

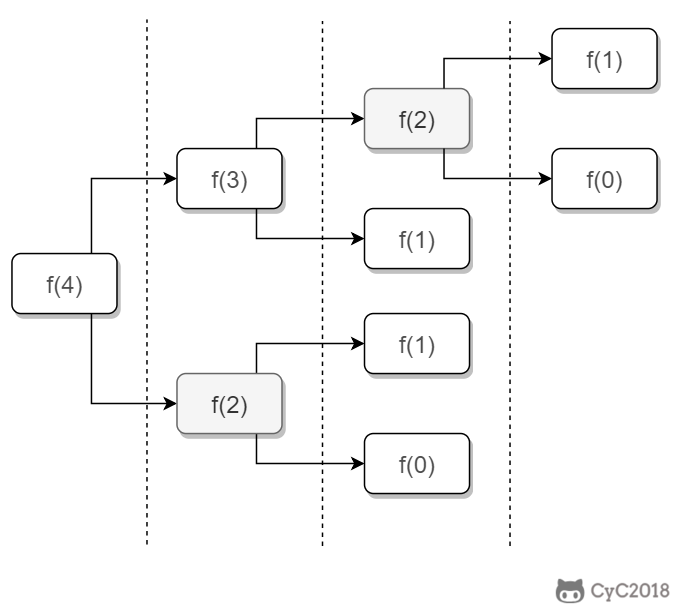
递归是将一个问题划分成多个子问题求解，动态规划也是如此，但是动态规划会把子问题的解缓存起来，从而避免重复求解子问题。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
package swordforoffer;

/**
 * @description:
 * @author: zw
 * @createDate: 2020/2/12
 * @version: 1.0.0
 */
public class Solution10 {

    // 使用递归
    public long fibonacci1(long n) {
        if (n == 0)
            return 0;
        if (n == 1)
            return 1;
        return fibonacci1(n - 1) + fibonacci1(n - 2);
    }

    // 使用动态规划
    public long fibonacci2(int n) {

        if (n <= 1)
            return n;

        long result = 0;
        long preOne = 0, preTwo = 1;
        // 注意起始下标位置
        for (int i = 2; i <= n; i++) {
            result = preOne + preTwo;
            preOne = preTwo;
            preTwo = result;
        }
        return result;
    }

    public static void main(String[] args) {
        Solution10 demo = new Solution10();
        System.out.println(demo.fibonacci1(0));
        System.out.println(demo.fibonacci2(0));
        System.out.println(demo.fibonacci1(2));
        System.out.println(demo.fibonacci2(2));
        System.out.println(demo.fibonacci1(8));
        System.out.println(demo.fibonacci2(8));
        // 递归真的超级慢
        System.out.println(demo.fibonacci1(50));
        System.out.println(demo.fibonacci2(50));
    }
}

青蛙跳台阶问题

题目1：一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

　　将跳法总数记为f(n)，可以知道f(1)=1，f(2)=2。当n>2时，第一次跳1级的话，还有f(n-1)种跳法；第一次跳2级的话，还有f(n-2)种跳法，所以可以推得f(n)=f(n-1)+f(n-2)，即为斐波那契数列。

题目2：一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

　　解法1：

　　当n=1时，f(1)=1。

　　当n大于1时，归纳总结可知：跳上n级台阶，第一次跳1级的话，有f(n-1)种方法；第一次跳2级的话，有f(n-2)种方法……第一次跳n-1级的话，有f(1)种方法；直接跳n级的话，有1种方法，所以可以得到如下公式：

　　f(n) = f(n-1)+f(n-2)+……f(1)+1　　（n≥2）

　　f(n-1) = f(n-2)+f(n-3)+…..f(1)+1　　（n>2）

　　由上面两式相减可得，f(n)-f(n-1)=f(n-1)，即f(n) = 2*f(n-1) (n>2)

　　最终结合f(1)和f(2)，可以推得：f(n)=2^(n-1)

　　解法2：

　　假设跳到第n级总共需要k次，说明要在中间n-1级台阶中选出任意k-1个台阶，即C(n-1,k-1)种方法。

　　所以：跳1次就跳上n级台阶，需要C(n-1,0)种方法；跳2次需要C(n-1,1)种方法……跳n次需要C(n-1,n-1)种方法

　　总共需要跳C(n-1,0)+C(n-1,1)+C(n-1,2)+……C(n-1,n-1)=2^(n-1)种方法。

　　解法3：

　　除了必须到达最后一级台阶，第1级到第n-1级台阶都可以有选择的跳，也就是说对于这n-1个台阶来说，每个台阶都有跳上和不跳上2种情况，所以一共有2^(n-1)种方法。

1
2
3
public int JumpFloorII(int target) {
    return (int) Math.pow(2, target - 1);
}

矩形覆盖问题

\题目：**用n个21的小矩形无重叠地覆盖一个2n的大矩形，总共有多少种方法？

　　当n = 1时，有一种方法。

　　当n = 2时，有两种方法。

　　当n >= 3时，和斐波那契数列类似。第一步竖着放，有f(n-1)种方法；第一步横着放，有f(n-2)种方法。所以f(n)=f(n-1)+f(n-2)。

小结

　　1.求n次方时，可以利用递归来降低时间复杂度

　　2.当遇到涉及n的问题时（类似青蛙跳台阶问题），注意f(n)与f(n-1)、f(n-2)等的关联，从而找出规律，进行合理建模。

　　3.return (int)Math.pow(2,target-1);

　　　　1) 转int类型

　　　　2）pow不是power

P82旋转数组查找最小值

思路

数组在一定程度上是排序的，很容易分析出：可以采用二分法来寻找最小数字。但是这里面有一些陷阱：

  1. 递增排序数组的本身是自己的旋转，则最小数字是第一个数字
  2. 中间数字与首尾数字大小相等，如{1,0,1,1,1,1}和{1,1,1,1,0,1}，无法采用二分法，只能顺序查找。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
package swordforoffer;

import javax.xml.bind.Element;

/**
 * @description: 旋转数组寻找元素
 * 例[4,5,6,7,1,2,3]中查找6
 * @author: zw
 * @createDate: 2020/1/29
 * @version: 1.0.0
 */
public class Solution11 {

    // 使用二分法
    public int findMinInRotateArray(int[] nums) {

        if (nums == null || nums.length <= 0)
            return 0;

        int low = 0, high = nums.length - 1;

        while (low < high) {
            int mid = low + (high - low) / 2;

            if (nums[low] == nums[mid] && nums[mid] == nums[high])
                return minNumber(nums, low, high);
                // 这里的两个和high/low的判断条件只用其中一个即可
            else if (nums[mid] <= nums[high])
                high = mid;
            else
                low = mid + 1;
        }
        return nums[low];
    }

    // 重写一遍
    public int findMinInRotateArray2(int[] nums) {
        // 判空
        if (nums == null || nums.length <= 0)
            return 0;

        int low = 0, high = nums.length - 1;

        // 这里直接比较数值，可直接剔除递增数组现象
        while (nums[low] >= nums[high]) {
            // 在low值和high值处满足"nums[low] >= nums[high] && high - low == 1"
            // 即两者相邻时，达到循环终止条件，返回第二个索引值即为最小值。
            if (high - low == 1) {
                return nums[high];
            }
            int mid = low + (high - low) / 2;
            // 特殊值处理，有相等值存在情况
            if (nums[high] == nums[mid] && nums[mid] == nums[low])
                return minNumber(nums, low, high);
                // 这两个判断条件是最初的特性判断
            else if (nums[mid] <= nums[high])
                high = mid;
            else if (nums[mid] >= nums[low])
                low = mid;
        }

        return nums[low];
    }

    private int minNumber(int[] nums, int l, int h) {
        for (int i = l; i < h; i++)
            if (nums[i] > nums[i + 1])
                return nums[i + 1];
        return nums[l];
    }

    // =======================测试代码===========================
    public void test1() {
        int[] array = null;
        System.out.println("test1:" + findMinInRotateArray(array) + findMinInRotateArray2(array));
    }

    public void test2() {
        int[] array = {};
        System.out.println("test2:" + findMinInRotateArray(array) + findMinInRotateArray2(array));
    }

    public void test3() {
        int[] array = {1};
        System.out.println("test3:" + findMinInRotateArray(array) + findMinInRotateArray2(array));
    }

    public void test4() {
        int[] array = {1, 2, 3, 4, 5, 6};
        System.out.println("test4:" + findMinInRotateArray(array) + findMinInRotateArray2(array));
    }

    public void test5() {
        int[] array = {2, 2, 2, 2, 1, 2};
        System.out.println("test5:" + findMinInRotateArray(array) + findMinInRotateArray2(array));
    }

    public void test6() {
        int[] array = {2, 1, 2, 2, 2, 2};
        System.out.println("test6:" + findMinInRotateArray(array) + findMinInRotateArray2(array));
    }

    public void test7() {
        int[] array = {6, 6, 8, 9, 10, 1, 2, 2, 3, 3, 4, 5, 6};
        System.out.println("test7:" + findMinInRotateArray(array) + findMinInRotateArray2(array));
    }

    public static void main(String[] args) {
        Solution11 demo = new Solution11();
        demo.test1();
        demo.test2();
        demo.test3();
        demo.test4();
        demo.test5();
        demo.test6();
        demo.test7();
    }
}

P89矩阵中的路径

题目

请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中任意一格开始，每一步可以在矩阵中向左、右、上、下移动一格。如果一条路径经过了矩阵的某一格，那么该路径不能再次进入该格子。例如在下面的3×4的矩阵中包含一条字符串“bfce”的路径（路径中的字母用下划线标出）。但矩阵中不包含字符串“abfb”的路径，因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后，路径不能再次进入这个格子。
A B T G
C F C S
J D E H

解题思路

使用回溯法（backtracking）进行求解，它是一种暴力搜索方法，通过搜索所有可能的结果来求解问题。回溯法在一次搜索结束时需要进行回溯（回退），将这一次搜索过程中设置的状态进行清除，从而开始一次新的搜索过程。例如下图示例中，从 f 开始，下一步有 4 种搜索可能，如果先搜索 b，需要将 b 标记为已经使用，防止重复使用。在这一次搜索结束之后，需要将 b 的已经使用状态清除，并搜索 c。

img

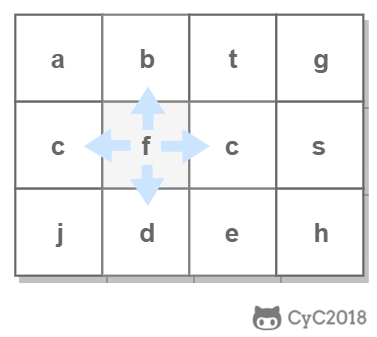
首先对所整个矩阵遍历，找到第一个字符，然后向上下左右查找下一个字符，由于每个字符都是相同的判断方法（先判断当前字符是否相等，再向四周查找），因此采用递归函数。由于字符查找过后不能重复进入，所以还要定义一个与字符矩阵大小相同的布尔值矩阵，进入过的格子标记为true。如果不满足的情况下，需要进行回溯，此时，要将当前位置的布尔值标记回false。（所谓的回溯无非就是对使用过的字符进行标记和处理后的去标记）

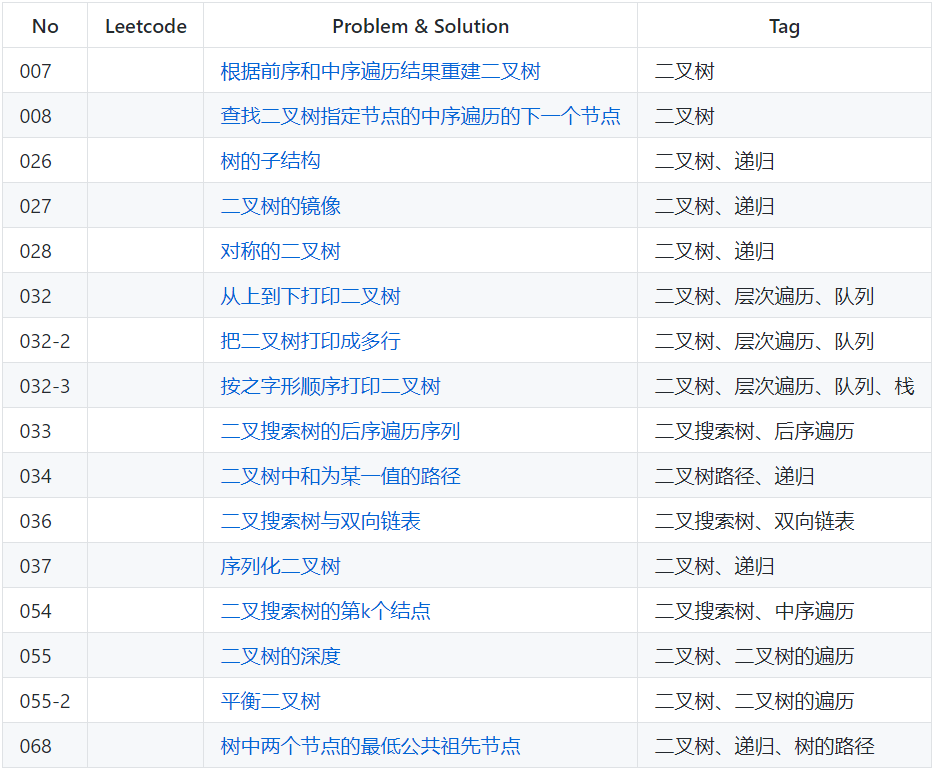
刷题类别：

二叉树

image-20200408151847430